How to Ensure Chat Security with OpenSSL

Protecting communication channels is extremely important for both business and private communications, since any breach can lead to a loss of sensitive information. Most popular messaging apps, including WhatsApp, Viber, and Telegram, use encryption to secure conversations. There are a variety of cryptographic algorithms available, however, and it can be challenging to choose the best way to protect your own messaging service.

This article provides recommendations on how to secure your chat or other message exchange protocol using popular and reliable cryptographic algorithms of the OpenSSL library. The article is aimed at people who are already familiar with basic encryption concepts and terminology but who don’t have a lot of experience with practical implementation.

Contents

Overview of Cryptographic Algorithms
How a Typical Secure Chat Application (WhatsApp, Telegram, Viber) Works
- General Scheme
- OpenSSL Code Example
Why Crypto Applications Should Be Open Source
Conclusion
References

Overview of Cryptographic Algorithms

Cryptographic algorithms are mathematical procedures or formulas used to encode information. Information is considered encrypted when it can be accessed only by the sender and the receiver. Even with cloud storage, properly encrypted data should be accessible only to the owner and should be inaccessible to the cloud service provider. This type of encryption is called zero-knowledge encryption, or private-key encryption.

The following types of algorithms are used for zero-knowledge encryption:

Hashes and PBKDF2
Asymmetric algorithms
Symmetric algorithms

There are a variety of Secure Hash Algorithms (SHAs) available. Old SHA1 algorithms are too simple for modern computers. SHA256 or SHA512 (varieties of SHA2) are currently the most popular hash functions used for cybersecurity. However, even SHA2 algorithms are too simple if they only use one iteration and don’t add a random sequence of bits called salt. The PBKDF2 function is more complex and, as a result, is widely used today for password hashing. PBKDF2 typically uses an SHA algorithm and salt to calculate a hash. A hash calculated with this method cannot be used in Rainbow or other attacks that rely on hacking hashes.

Asymmetric algorithms are very slow and cannot be used for encryption of large amounts of data. So in most cases, they’re used to encrypt the keys of symmetric algorithms. The most popular asymmetric algorithms are Rivest–Shamir–Adleman (RSA) and Elliptic-curve Diffie–Hellman (ECDH).

The Advanced Encryption Standard (AES) is the absolute winner in the world of symmetric algorithms. It’s used almost everywhere. It’s fast, has lots of implementations in different languages, and modern CPUs hardware even have built-in support for it.

Certificates are another important part of secure data exchange between the server and the client. Without certificate validation, there’s no way to know that a connection is actually secure. Certificates are essentially a system of asymmetric algorithms that validate the server.

Related services

Engineering for Cybersecurity Projects

How a Typical Secure Chat Application (WhatsApp, Telegram, Viber) Works

General Scheme

To provide a secure connection between two users, it’s important to take into account all steps in using a messaging app, from registration to actually sending messages. There are four steps to exchanging messages:

Registration (Figure 2)
Login (Figures 3 and 4)
Adding a user to a contact list (Figure 5)
Exchanging messages (Figure 6)

For the registration procedure, your application should request the server’s keys so that user data can be handled securely:

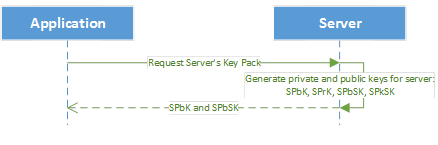
Figure 1: Pre-registration action for request to verify server keys

Figure 1 shows what keys the application requests from the server to use for registration, login, and other interactions with the server. These keys are required to verify and encrypt data exchanged with the server. After this request, all user data must be encrypted with the server’s keys.

The server generates the following keys:

SPbK – server public key (RSA or ECDH)

SPrK – server private key (RSA or ECDH)

SPbSK – server public signing key (RSA or ECDSA)

SPrSK – server private signing key (RSA or ECDSA)

The SPbK should be used to encrypt session keys or any other small amounts of secure information that should be understood only by the server.

During registration, the program generates all necessary keys and then sends them to the server in an encrypted state. The private key should be sent to the server in case the user logs in from a different device. Keys are encrypted with a master key that never leaves the user’s device, which means that they cannot be decrypted on the server side.

Here’s a diagram of this process:

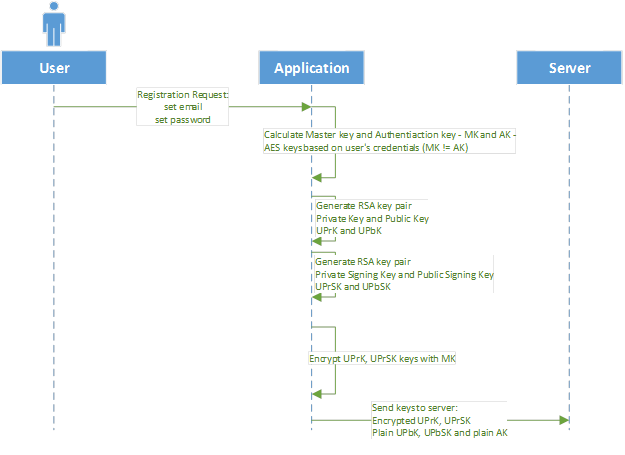
Figure 2: Registration process

As you can see in Figure 2, all private data that’s sent to the server is encrypted with the master key based on the user’s credentials, so it cannot be decrypted by the server.

After this point, all other data can be exchanged more securely with the user keys. The server can use the PbK to encrypt a session key.

Figure 3: Session key and server verification

Once registration has been completed successfully, the user has the following keys:

Authentication key(AK). This key is used for authentication, and the client application must send it to the server. The server authenticates the user with this key. The AK is generated with the PBKDF2 function, and it must be different than the master key. Here’s an example of how the AK can be generated: AK=PBKDF2(password, user’s email as salt, 10000)
Master key (MK). This key is used to encrypt and decrypt a user’s key pack. It must not be sent to the server or anywhere else. The MK must be kept locally. Here’s an example of how the MK can be generated: MK=PBKDF3(password, username + “@” + domain + username as salt, 20000)
User’s private key (UPrK)
User’s private key for signing (UPrSK)
User’s public key (UPbK)
User’s public key to check signatures (UPbSK)
Server’s public key (SPbK)
Server’s public key to check signatures (SPbSK)
Session key to encrypt all data that will go to server (SK)

The session key is required to speed up data decryption between the server and the device. Asymmetric algorithms aren’t suitable in this situation due to their slowness.

Let’s say that the user wants to log in from a new device. Here’s how that works:

Figure 4: Login process

Now the user has all of their keys and is able to start chatting with other users. As you can see, the user’s password in memory is required for generating the AK and MK. If the user logs in from a new device, the application will request the server’s keys and use them to encrypt the AK (Figure 1).

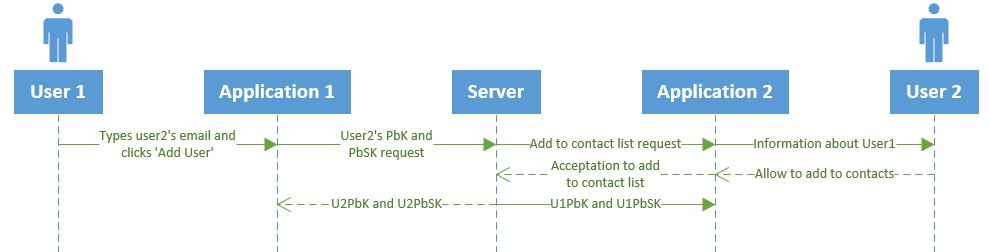
Figure 5: Users’ key exchange

The original user (User 1) now has information about the public keys of the person they initiated communication with (User 2). These keys are used for secure chatting. All data encrypted with these keys will be available only for these two users.

And now these users can send messages to each other:

Figure 6: Chatting

The same logic for encrypting messages applies to User 2: encrypt a message with the SK and send it to User 1. If it’s necessary to send some large binary data, then this data can contain its own data key and this data key can be encrypted with the users’ public keys.

OpenSSL Code Example

If you want to build a secure chat application, you can secure your programming with OpenSSL. All functions in OpenSSL are well-documented, and it’s usually easy to find examples and descriptions. Let’s look at our example of secure chat application development.

Here’s a list of some operations that were used in the encryption process above:

1. Prepare master key

2. Generate user’s public and private keys for encryption

3. Encrypt and decrypt using AES

4. Encrypt key pairs

5. Sign message with RSA

6. Verify signature information

All functions below use the OpenSSL API.

The image below shows how to generate a master key based on a password and a user’s email.

C++

void GeneratePbkdf2Sha256Hash(const std::string& username, 
                              const std::string& domain, 
                              const std::string& password, 
                              /*OUT*/ Bytes_vt& passwordHash)
{
    const int kPasswordHashIterationNumber = 10000;
    const int kPasswordHashSize = 32;
   
    std::string salt(userName + "@" + domain + userName);
   
    passwordHash.resize(kPasswordHashSize);
     
    int result = PKCS5_PBKDF2_HMAC(password.c_str(),
                     static_cast<int>(password.size()),
                     reinterpret_cast<const unsigned char*>(salt.data()),
                     static_cast<int>(salt.size()),
                     iterationsNumber,
                     EVP_sha256(),
                     static_cast<int>(passwordHash.size()),
                     reinterpret_cast<unsigned char*>(passwordHash.data()));
     
    if (1 != result)
    {
        int errorCode = static_cast<int>(ERR_get_error());
        throw OpensslException(errorCode, ERR_error_string(errorCode, NULL));
    }
}

This next image shows how to generate RSA keys. These will be used as the user’s public and private keys for encryption and signing. RSA_generate_key is the OpenSSL function that actually generates keys.

C++

struct RsaKeyPair
{
Bytes_vt n; //public modulus
Bytes_vt e; //public exponent
Bytes_vt d; //private exponent
Bytes_vt p; //first secret prime factor
Bytes_vt q; //second secret prime factor
Bytes_vt dmp1; //dmp1 in RSA struct
Bytes_vt dmq1; //dmq1 in RSA struct
Bytes_vt iqmp; //iqmp in RSA struct
};
void BignumToBinary(BIGNUM* bignum, Bytes_vt& binary)
{
    binary.resize(BN_num_bytes(bignum));
    BN_bn2bin(bignum, reinterpret_cast<unsigned char*> (&binary.at(0)));
}
void GenerateRsaKeyPair(RsaKeyPair& rsaKeyPair)
{
    std::shared_ptr<RSA> rsaWrapper(
RSA_generate_key(kRsaKeySizeBits, kRsaPublicExponent, NULL, NULL), 
RSA_free);
    BignumToBinary(rsaWrapper->n, rsaKeyPair.n);
    BignumToBinary(rsaWrapper->e, rsaKeyPair.e);
    BignumToBinary(rsaWrapper->d, rsaKeyPair.d);
    BignumToBinary(rsaWrapper->p, rsaKeyPair.p);
    BignumToBinary(rsaWrapper->q, rsaKeyPair.q);
    BignumToBinary(rsaWrapper->dmp1, rsaKeyPair.dmp1);
    BignumToBinary(rsaWrapper->dmq1, rsaKeyPair.dmq1);
    BignumToBinary(rsaWrapper->iqmp, rsaKeyPair.iqmp);
}

The code below shows a simple class that hides OpenSSL AES encryption and provides a simple interface to use it:

C++

static const int kAesIvSize = AES_BLOCK_SIZE; // AES_BLOCK_SIZE is from openssl/aes.h and equals 16
AesGcmCryptor::AesGcmCryptor(const Byte* aesKey, size_t keySizeInBytes, const Bytes_vt& initializationVector)
    : m_aesKey(aesKey, aesKey + keySizeInBytes)
    , m_iv(initializationVector) {}
void aesGcmEncrypt(const Byte* plainBytes, size_t plainBytesSize, Bytes_vt& cipherBytes) {
    cipherBytes.resize(plainBytesSize);
    CipherContextGuard ctxGuard(EVP_CIPHER_CTX_new());
    EVP_EncryptInit_ex(ctxGuard.getContext(), 
EVP_aes_256_gcm(), 
NULL, 
NULL, 
NULL);
    /* Set IV length if default 12 bytes (96 bits) is not appropriate */
    EVP_CIPHER_CTX_ctrl(ctxGuard.getContext(), 
EVP_CTRL_GCM_SET_IVLEN, 
static_cast<int>(m_iv.size()), 
NULL);
    /* Initialise key and IV */
    EVP_EncryptInit_ex(ctxGuard.getContext(), NULL, NULL, 
reinterpret_cast<unsigned char*>(&m_aesKey.at(0)), 
reinterpret_cast<unsigned char*>(&m_iv.at(0)));
    /* Provide the message to be encrypted, and obtain the encrypted output.
     * EVP_EncryptUpdate can be called multiple times if necessary */
    int len;
    EVP_EncryptUpdate(ctxGuard.getContext(), 
reinterpret_cast<unsigned char*>(&cipherBytes.at(0)), 
&len,
reinterpret_cast<const unsigned char*>(plainBytes), 
static_cast<int>(plainBytesSize));
    /* Finalize the encryption. Normally ciphertext bytes may be written at
     * this stage, but this does not occur in GCM mode */
    EVP_EncryptFinal_ex(ctxGuard.getContext(), 
reinterpret_cast<unsigned char*>(&cipherBytes.at(0)) + len, 
&len);
    /* Get the tag */
    Bytes_vt tagBytes(kAesGcmTagSize);
    EVP_CIPHER_CTX_ctrl(ctxGuard.getContext(), 
EVP_CTRL_GCM_GET_TAG, 
kAesGcmTagSize,
reinterpret_cast<unsigned char*>(&tagBytes.at(0)));
    cipherBytes.insert(cipherBytes.end(), tagBytes.begin(), tagBytes.end());
}

Here’s an example of AES decryption:

C++

void aesGcmDecrypt(const Byte* cipherBytes, size_t cipherBytesSize, Bytes_vt& plainBytes) {
    size_t plainBytesSize = cipherBytesSize - kAesGcmTagSize;
    plainBytes.resize(plainBytesSize);
    CipherContextGuard ctxGuard(EVP_CIPHER_CTX_new());
    EVP_DecryptInit_ex(ctxGuard.getContext(), EVP_aes_256_gcm(), 0, 0, 0);
    /* Set IV length if default 12 bytes (96 bits) is not appropriate */
    EVP_CIPHER_CTX_ctrl(ctxGuard.getContext(), 
EVP_CTRL_GCM_SET_IVLEN, 
static_cast<int>(m_iv.size()), 
NULL);
    /* Initialize key and IV */
    EVP_DecryptInit_ex(ctxGuard.getContext(), 
NULL, 
NULL, 
reinterpret_cast<unsigned char*>(&m_aesKey.at(0)),
reinterpret_cast<unsigned char*>(&m_iv.at(0)));
    /* Provide the message to be decrypted, and obtain the plaintext output.
     * EVP_DecryptUpdate can be called multiple times if necessary */
    int len;
    EVP_DecryptUpdate(ctxGuard.getContext(), 
reinterpret_cast<unsigned char*>(plainBytes.data()), 
&len,
reinterpret_cast<const unsigned char*>(cipherBytes), 
static_cast<int>(plainBytesSize));
    int plaintext_len = len;
    /* Set expected tag value.*/
    char tag[kAesGcmTagSize];
    memcpy(tag, cipherBytes + cipherBytesSize - kAesGcmTagSize, kAesGcmTagSize);
    EVP_CIPHER_CTX_ctrl(ctxGuard.getContext(), EVP_CTRL_GCM_SET_TAG, kAesGcmTagSize, tag);
    /* Finalize the decryption. A positive return value indicates success,
     * anything else is a failure - the plaintext is not trustworthy.
     */
    EVP_DecryptFinal_ex(ctxGuard.getContext(), 
reinterpret_cast<unsigned char*>(plainBytes.data()) + len, 
&len);
    plaintext_len += len;
    plainBytes.resize(plaintext_len);
}

The following shows encryption of key pairs that were generated using the function above:

C++

Bytes_vt EncryptBytesUsingAesGcm(const Byte* plainBytes, 
size_t plainBytesSize, 
const Bytes_vt& aesKey, 
const Bytes_vt& iv)
{
    Bytes_vt cipherBytes;
    crypto::AesGcmCryptor cryptor(aesKey.data(), aesKey.size(), iv);
    cryptor.encrypt(plainBytes, plainBytesSize, cipherBytes);
    return cipherBytes;
}
Bytes_vt encryptPrivateKeys(const RsaKeyPair& encryptDecryptKeyPair, 
const RsaKeyPair& signVerifyKeyPair, 
const Bytes_vt& encryptionKey)
{
    Bytes_vt pdkIv(kAesIvSize);
    GenerateRandomBytes(pdkIv.data(), pdkIv.size());
    Bytes_vt pskIv(kAesIvSize);
    GenerateRandomBytes(pskIv.data(), pskIv.size());
    std::string encryptDecryptString = KeyToString(encryptDecryptKeyPair);
    std::string signVerifyString = KeyToString(signVerifyKeyPair);
     
    Bytes_vt encryptedPdk = EncryptBytesUsingAesGcm(encryptDecryptString.c_str(), 
    encryptDecryptString.size(), 
encryptionKey, 
pdkIv);
    Bytes_vt encrytedPsk = EncryptBytesUsingAesGcm(signVerifyString.c_str(), 
signVerifyString.size(), 
encryptionKey, 
pskIv);
    uint16_t encryptedPdkLen = static_cast<uint16_t>(encryptedPdk.size());
    Bytes_vt privateKeysBlob(sizeof(encryptedPdkLen) + pdkIv.size() + pskIv.size() + 
encryptedPdk.size() + encrytedPsk.size());
    privateKeysBlob[0] = static_cast<Byte>(encryptedPdkLen % 0x100);
    privateKeysBlob[1] = static_cast<Byte>(encryptedPdkLen / 0x100);
    auto it = privateKeysBlob.begin() + sizeof(encryptedPdkLen);
    it = std::copy(pdkIv.begin(), pdkIv.end(), it);
    it = std::copy(pskIv.begin(), pskIv.end(), it);
    it = std::copy(encryptedPdk.begin(), encryptedPdk.end(), it);
    it = std::copy(encrytedPsk.begin(), encrytedPsk.end(), it);
    return privateKeysBlob;
}

The image below shows how to sign outgoing data using RSA:

C++

void rsaSign(
const Byte* source, 
size_t sourceSize, 
Bytes_vt& signature,
RSA* rsa)
{
    unsigned char hash[SHA256_DIGEST_LENGTH];
    SHA256_CTX sha256Context = {0};
    SHA256_Init(&sha256Context);
    SHA256_Update(&sha256Context, source, sourceSize);
    SHA256_Final(hash, &sha256Context);
    signature.resize(RSA_size(m_rsa.get()));
    unsigned int signatureResultSize = 0;
    int result = RSA_sign(NID_sha256, 
hash, 
sizeof(hash), 
reinterpret_cast<unsigned char*> (&signature.at(0)), 
&signatureResultSize, 
rsa);
    if (1 != result)
    {
        _THROW_WITH_DEFAULT_INFO;
    }
    if (signatureResultSize != signature.size())
    {
        _THROW(cryptoErrorSigning);
    }
}

And here’s how to verify data on the other side:

C++

bool rsaVerify(
const Byte* source, 
size_t sourceSize, 
const Byte* signature, 
size_t signatureSize, 
RSA* rsa)
{
    unsigned char hash[SHA256_DIGEST_LENGTH];
    SHA256_CTX sha256Context = {0};
    SHA256_Init(&sha256Context);
    SHA256_Update(&sha256Context, source, sourceSize);
    SHA256_Final(hash, &sha256Context);
    int result = RSA_verify(NID_sha256, 
hash, 
sizeof(hash), 
reinterpret_cast<const unsigned char*> (signature), 
static_cast<int> (signatureSize), 
rsa);
    return (1 == result);
}

Why Crypto Applications Should Be Open Source

When somebody says that an application can’t be hashed, that’s actually not true. We all remember the issue in OpenSSL that affected all applications that use this library as their main cryptographic module. Only the public availability of the OpenSSL programming examples makes it possible to find such security holes.

Sometimes, people try to implement their own AES algorithms or other algorithms. However, it’s very dangerous to use such libraries. And if authors of a library don’t provide the source code, then it’s best not to touch it at all because nobody can verify the correctness of the algorithm inside. Unknown libraries may contain a lot of vulnerabilities that allow perpetrators access to your application.

The same goes for applications that claim to be secure. If no one can see the code, then such claims can’t be verified. Consumers may not trust your security because the source code isn’t publicly available.

It’s a good idea to prepare a separate library that contains all security logic and make it available to everyone.

Related services

Data Management Solutions

Conclusion

In this article, we’ve covered the security principles behind encrypting instant message communications between two users. OpenSSL is the library of choice for most use cases, and we’ve provided detailed example of how to use it. The encryption scheme we’ve described proves effective in most cases and can be easily modified according to software requirements.

Communication security is a pretty wide issue, and it can take a lot of time to cover all the nuances of implementation. In this article, we’ve covered only how to securely transport messages from user to user, but you should also keep the following in mind when designing your own chat app:

Server-side security and how to securely store passwords in a database (not as plain text, of course)
Client-side caching of security data
Generating salt
Choosing cryptographic algorithms

You can learn more about our experience using OpenSSL programming for data encryption here.

The Apriorit team has also developed our own data encryption technologies. We would be glad to assist you with data encryption for your communication software. Get in touch!